Gallery

This synthetic experiment measures the (log-scaled) runtime and relative error of approximate MPO-MPS contraction algorithms with respect to a precomputed machine-accuracy contract-then-compress baseline. The input MPS and MPO are populated with uniformly random entries in \([\alpha,1]\) for \(\alpha=-0.5\). Both the MPO and MPS are $n=100$ tensors long with uniform MPO/MPS bond dimension $50$. Complete code for all of the methods in this plot can be found here, and here.

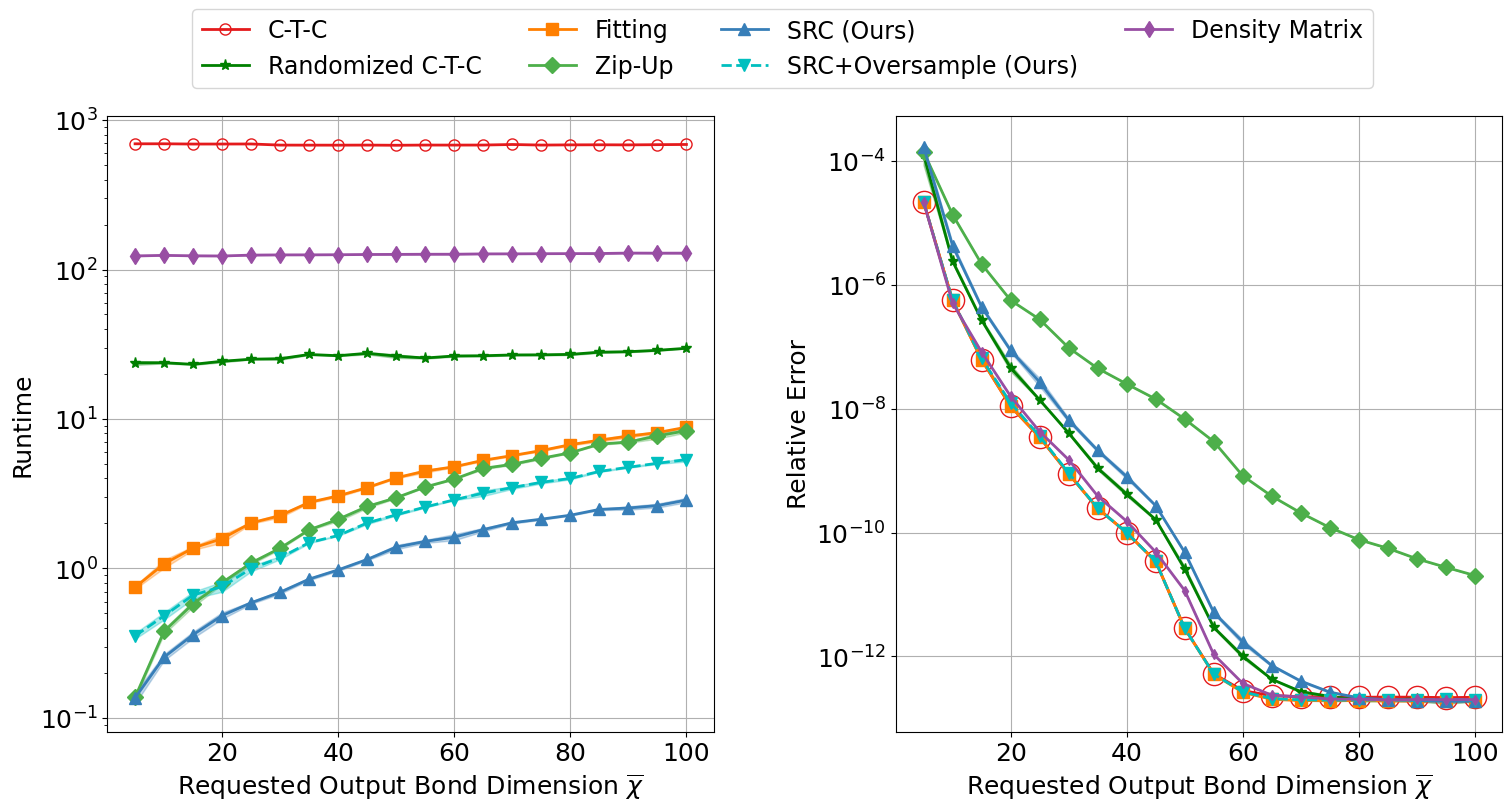
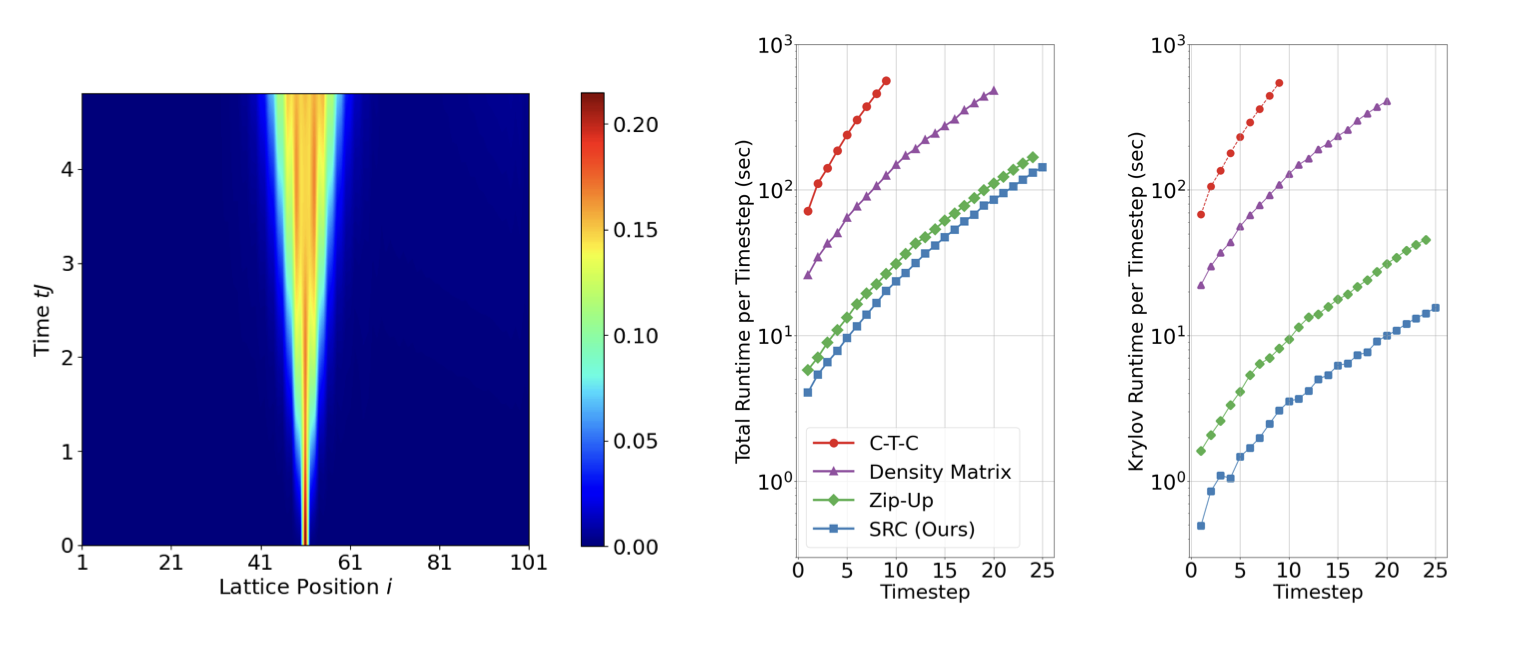
To demonstrate the effectiveness of SRC, we simulate the unitary time evolution \[ |\boldsymbol{\psi}(t)\rangle = \mathrm{e}^{-i t \mathbf{H}}\,|\boldsymbol{\psi}(0)\rangle \] starting from a locally preturbed initial state vector of $n=101$ spins \[ |\boldsymbol{\psi}(0)\rangle = \mathrm{e}^{i(\pi/4)\,\mathbf{Y}_{\lceil n/2\rceil}}\,|\boldsymbol{\psi}_{\min}\rangle\in \mathbb{C}^{2^{101}}, \] under the long‐range interacting XY Hamiltonian \[ \mathbf{H} = \frac{1}{2}\sum_{1 \le i < j \le n} \frac{J}{|i - j|^{1.5}}\bigl(\mathbf{X}_i\mathbf{X}_j + \mathbf{Y}_i\mathbf{Y}_j\bigr)\in \mathbb{C}^{2^{101}\times 2^{101}}. \] Here, \(|\boldsymbol{\psi}_{\min}\rangle\) is the ground state of \(\mathbf{H}\) obtained via DMRG-2. We then examine the magnetization dynamics of this defected system using the Time-Dependent Variational Principle with Ancillary Krylov Subspace method (GSE-TDVP1). GSE-TDVP1 builds a Krylov space \(\mathcal{K}\) from compressed MPO–MPS products and uses it to enrich the MPS at each timestep—an extension of the original TDVP algorithm. Additional details for this experiment can be found in the full paper.

Full Python implementations are available here:

• DMRG-2 implementation
• GSE-TDVP1 implementation